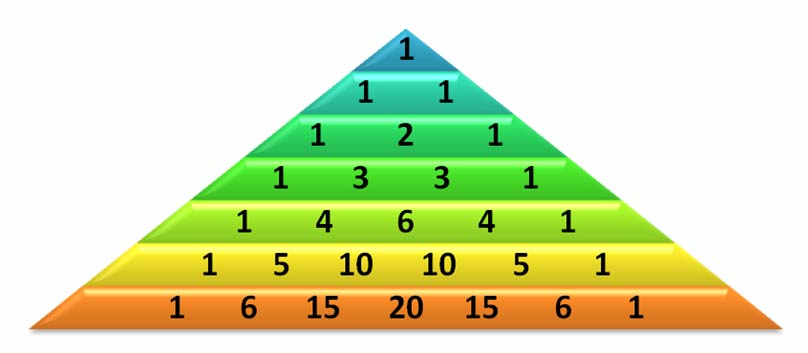
Pascal's triangle is a useful recursive definition that tells us the coefficients in the expansion of the polynomial (x + a)^n. Each element in the triangle has a coordinate, given by the row it is on and its position in the row (which you could call a column). Every number in Pascals triangle is defined as the sum of the item above it and the item above it and to the left. If there is a position that does not have an entry, we treat it as if we had a 0 there. Given the following recursive function signature, write down the recursive function which takes a row and a column and finds the value at that position in the triangle. Consider that the triangle starts at row 0 and column 0.
int pascal(int row, int column) { }